For this part, I’d like to dive into Kalman Filter. As it is absolutely necessary to understand it, atleast partly to implement MonoSlam. For the first few sections, I’ll talk about Gaussian Distribution, Kalman Filter and demonstrate a simple and famous 1D Car example to demonstrate it. Later I’ll draw parallels between our example and MonoSlam. So lets get started.
Gaussian Noise
Imagine a archer taking a shot at a target. Now, a well versed archer has more chances of hitting the center or near the center of target and a less experienced one might hit all over the place.
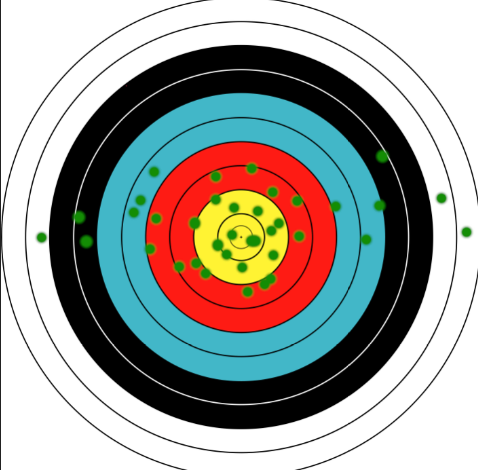
If we plot a graph of x-coordinates of these hits, we’ll get a curve similar to this. This curve represents a natural distribution of a variable that is trying to achieve a target value. This is called a Gaussian curve. The steepness of the curve shows how spread out the values can be, and the mean of all the values give us the target value of the distribution. In a way it represents probability of a variable with a target value(mean).
Kalman Filter
Kalman filter is an algorithm for state estimation. The algorithm provides a way to estimate current state from what the previous state was and what the sensors is observing. The estimation from previous state is called Prediction and correcting this prediction using sensor values is called Measurement. I picked this article which explains it in detail and this crash course to understand how to set up a simple Unity3D project to demo it. It is important to go thru those two references to understand everything below!
1D Car in Unity3D!
To start working on Unity3D example, first thing we need is a matrix library to do all the matrix operations. Unfortunately there is no straightt forward generic C# library to do this. So, I wrote my own.
public class Matrix
{
///Number of rows in matrix
private int _rows;
public int rows {get { return _rows; }}
///Number of columns in matrix
private int _columns;
public int columns { get { return _columns; } }
///Data
private List<List<float>> elements;
//Constructor
public Matrix(int rows, int columns)
;
//Indexing the Matrix
public float this[int r, int c];
//Log matrix
public string Print();
/// <summary>
/// Returns square identity matrix of specified size
/// </summary>
/// <param name="size"> size of identity matrix </param>
/// <returns></returns>
public static Matrix Identity(int size);
//Matrix Additions
public static Matrix operator +(float v, Matrix a);
public static Matrix operator +(Matrix a, float v);
public static Matrix operator +(Matrix a, Matrix b);
//Matrix Substractions
public static Matrix operator -(Matrix a, float v);
public static Matrix operator -(float v, Matrix a);
public static Matrix operator -(Matrix a, Matrix b);
//Matrix multipications
public static Matrix operator *(float v, Matrix a);
public static Matrix operator *(Matrix a, float v);
public static Matrix operator *(Matrix a, Matrix b);
//Matrix transpose
public Matrix Transpose();
//if Matrix of size 1x1 returns the element
public float Value();
//calculate inverse of matrix
public Matrix Inverse();
}The implementations of the methods are rather long, but you can find implentations in the github. I wanted to make it generic class but unfortunately the multiplication and addition operations cannot be done in generic types, even with constraints.
With the matrix operations set up, lets create a car! I used this 3D model and attached CarRealWorld script to it. Since we are simulating a real world car, there is noise in the system, which we need to generate. Now remember, Kalman Filter is all about reading these different noise filled states and predicting a state of current system. So to simulate a real world car, with a input of accelaration, would look something like this:
public class CarRealWorld : MonoBehaviour
{
public float accelerationNoise;
public float positionNoise;
private float velocity;
private float _acceleration;
public float acceleration {
get {
return _acceleration;
}
set {
//Input sensor inaccuracy
_acceleration = Mathf.Clamp(value + Gaussian.RandomGaussian() * accelerationNoise, 0, Mathf.Infinity);
}
}
private float _position;
public float position {
get {
//GPS inaccuracy
return transform.position.x + Gaussian.RandomGaussian() * positionNoise;
}
set
{
_position = value;
transform.position = new Vector3(_position, 1 ,0);
}
}
private void Start()
{
velocity = 0;
acceleration = 0;
position = 0;
}
// Update is called once per frame
void Update()
{
OneStep(Time.deltaTime);
if (Input.GetKey(KeyCode.A))
{
acceleration = 50;
}
else {
acceleration = 0;
}
}
public void OneStep(float deltaTime) {
position = _position + (velocity * deltaTime) + (_acceleration * deltaTime * deltaTime);
velocity = velocity + (_acceleration * deltaTime * deltaTime);
}
public float GetGPSPosition() {
return position;
}
}
Here noise is simulated when reading position i.e. our GPS and setting acceleration i.e. our input. In real world the noise should more only when input is started or ended but we will put it thruout. To move the car, in each step we simply modify the position using current velocity and accelerations.
Now, assume we are trying to mimic this real world car in software, so we setup code to take accelration input reading and update our car position. This car will represent what happens if we just take the accelerator input and put it in our system. We can call this CarAccelerationInput.
public class CarAccelerationInput : MonoBehaviour
{
public CarRealWorld car;
float velocity;
float acceleration;
float position
{
get
{
return transform.position.x;
}
set
{
transform.position = new Vector3(value, 5, 0);
}
}
// Start is called before the first frame update
void Start()
{
velocity = 0;
position = 0;
}
// Update is called once per frame
void LateUpdate()
{
OneStep(Time.deltaTime);
}
public void OneStep(float deltaTime) {
acceleration = car.acceleration;
position += (velocity * deltaTime) + (acceleration * deltaTime * deltaTime);
velocity += acceleration * deltaTime * deltaTime;
}
}This car, just gets the acceleration input from our real world car in each step and updates the position. You will see this is not a good setup to track car as it takes noisy readings.
At last, we create another car simulation with Kalman Filter. This system accounts for noises and is much more robust. Here is how the Kalman prediction looks like.
public class KalmanFilter : MonoBehaviour
{
public CarRealWorld car;
//state vector mean
public Matrix x_cap_Current;
//state vector covariance
public Matrix P_cap_Current;
//Jacobian matrix
public Matrix JacobianMatrix_H;
// Every step we calculate these two
//state vector mean
public Matrix x_cap_New;
//state vector covariance
public Matrix P_cap_New;
//Prediction (Intermidiate results)= checks
//state vector mean
public Matrix x_K_check_New;
//state vector covariance
public Matrix P_K_check_New;
public float Q;
public float R;
//Function F = previous state estimate processing matrix
Matrix FunctionMatrix_F(float deltaTime) {
Matrix FunctionMatrix_F = new Matrix(2,2);
FunctionMatrix_F[0, 0] = 1;
FunctionMatrix_F[0, 1] = deltaTime;
FunctionMatrix_F[1, 0] = 0;
FunctionMatrix_F[1, 1] = 1;
return FunctionMatrix_F;
}
//Function G = input processing matrix
Matrix FunctionMatrix_G(float deltaTime) {
Matrix FunctionMatrix_G = new Matrix(2, 1);
FunctionMatrix_G[0, 0] = deltaTime * deltaTime;
FunctionMatrix_G[1, 0] = deltaTime;
return FunctionMatrix_G;
}
//covariance in motion model noise
Matrix CovarianceMatrix_Q() {
return Matrix.Identity(2) * Q;
}
//covariance in measurement model
Matrix CovarianceMatrix_R()
{
return Matrix.Identity(1) * R;
}
//input accelaration from user
Matrix input_acceleration_current() {
//input accelaration
Matrix input_acceleration_current = new Matrix(1, 1);
input_acceleration_current[0, 0] = car.acceleration;
return input_acceleration_current;
}
//GPS Measurement
Matrix y1_GPS() {
// y1
Matrix y1 = new Matrix(1, 1);
y1[0, 0] = car.position;
return y1;
}
// Start is called before the first frame update
void Start()
{
// Input data! => Assumptions
x_cap_Current = new Matrix(2,1);
//start position
x_cap_Current[0, 0] = 0;
//start velocity m/s
x_cap_Current[1, 0] = 0;
// Input state covariance => P
P_cap_Current = new Matrix(2, 2);
P_cap_Current[0, 0] = 0.01f;
P_cap_Current[0, 1] = 0f;
P_cap_Current[1, 0] = 0f;
P_cap_Current[1, 1] = 1f;
//Jacobian matrix H
JacobianMatrix_H = new Matrix(1, 2);
JacobianMatrix_H[0, 0] = 1;
JacobianMatrix_H[0, 1] = 0;
}
// Update is called once per frame
void LateUpdate()
{
OneStep(Time.deltaTime);
transform.position = new Vector3(x_cap_Current[0,0], -1 , 0);
}
void Prediction(float deltaTime) {
x_K_check_New = (FunctionMatrix_F(deltaTime) * x_cap_Current) + (FunctionMatrix_G(deltaTime) * input_acceleration_current());
P_K_check_New = (FunctionMatrix_F(deltaTime) * (P_cap_Current * FunctionMatrix_F(deltaTime).Transpose())) + CovarianceMatrix_Q();
}
void Correction() {
// calculate gain
Matrix K = (P_K_check_New * JacobianMatrix_H.Transpose()) * ((JacobianMatrix_H * (P_K_check_New * JacobianMatrix_H.Transpose())) + CovarianceMatrix_R()).Inverse();
// fuse prediction and correction
// (y1_GPS - (JacobianMatrix_H * x_K_check_New)) is the innovation
x_cap_New = x_K_check_New + K * (y1_GPS() - (JacobianMatrix_H * x_K_check_New));
P_cap_New = (Matrix.Identity(2) - (K * JacobianMatrix_H)) * P_K_check_New;
}
void OneStep(float deltaTime)
{
Prediction(deltaTime);
Correction();
//update state
x_cap_Current = x_cap_New;
P_cap_Current = P_cap_New;
}
}With this simple code to do 1D Kalman predictions we can see in the output how the filter keeps track of real world car. Modifying the sensor covariances Q and R will show how differently the Kalman can predict position of car based on sensor noise. Here is how the output looks like:
Now this is a 1D system with a linear Kalman filter. For MonoSLAM we will be needing Extended Kalman Filter which deals with non linear system. But for now to draw parallels here, our state vector and covariance matrix in MonoSLAM are as following:
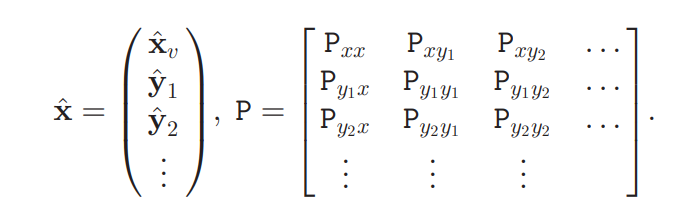
where
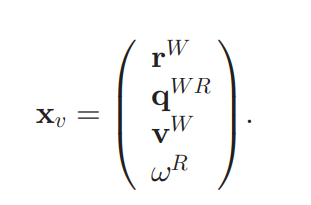
The input to the system is an unknown linear acceleration and unknown angular acceleration. These accelerations will be gaussian with mean equaling most probable path the camera is going to take.
For the correction step we use the features we observe using camera. For now assume camera is able to see every unique feature in the environment and store its position in map for look up. Every step we check where the markers are observed now and use this to adjust our prediction.
I’ll expand more on this later! Been a busy week!
All of this is quiet a lot of math to implement, so I’m not sure if I can learn all this new math by next week lol! So I’ll probably pick this up at a later time.
NOTE: I’m travelling next week so expect delays in new posts! (bold of me to assume you are waiting for me lol!)